3443：【2024年5月】7级算法等考第3题 最多感染的牛数量

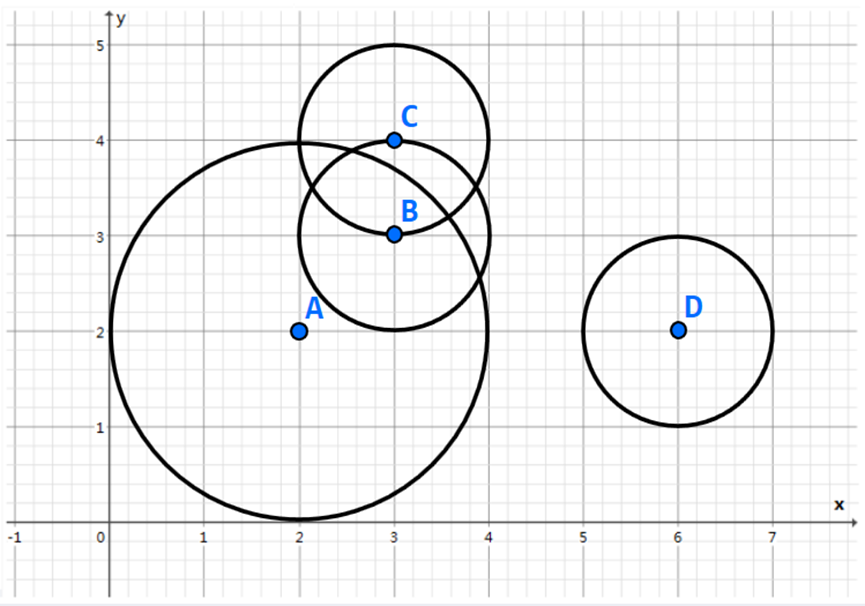
## Description 有一片农场，可以将其视为一个直角坐标平面图。农场上分布着n头牛，其中第i头牛的位置坐标为（xi，yi）。有一天其中一头牛感染了某种病毒，并在其周围形成一片感染区域，感染区域定义为以该牛为圆心，半径为ri的圆形，处于这个区域内（包括区域边缘）的其他牛都会被感染，这些被感染的牛同样会形成感染区域进一步感染更多的牛，由于每头牛的体质不一样，所以感染区域的半径可能也不一样。 假设这些牛的位置不发生变化，如果最初只有一头牛被感染的情况下，最终被感染的牛的数量的最大值是多少？ 例如：n = 4； 这4头牛的位置坐标分别为（2，2），（3，3），（3，4） ，（6，2）； 它们被感染后各自形成的感染区域的半径分别是2，1，1，1。 如下图所示：  由上图可知，如果最初只有D被感染，最终只有1头牛（D）被感染；如果最初B或C被感染，最终都会有2头牛（B、C）被感染，如果最初A被感染，最终会有3头牛（A、B、C）被感染，故最大数量为3。 ## Input Format 第一行包含一个整数n，表示农场上牛的数量； 接下来n行，每行包含3个整数xi，yi，ri，分别表示第i头牛的横坐标、纵坐标以及被感染后形成的感染半径，整数之间以一个空格隔开。 数据范围 测试点1~10：1≤n≤100，1≤xi,yi,ri≤105。 ## Output Format 一个整数，表示最初只有一头牛被感染的情况下，最终被感染的牛的数量的最大值。 ```input1 4 2 2 2 3 3 1 3 4 1 6 2 1 ``` ```output1 3 ```