3304：推理

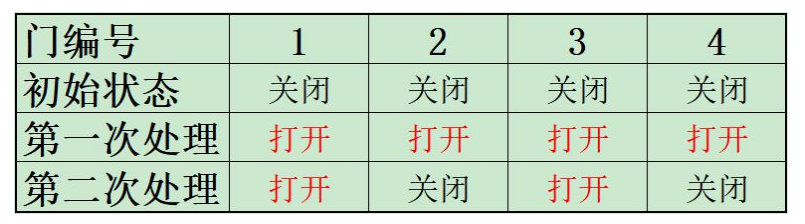
## 题目描述 某校有 $N$ 间教室，且每间教室有 $2$ 扇门，一共有 $2 \times N$ 扇门，每扇门都有编号，分别从 $1$ 到 $2 \times N$。 开始时，所有门为关闭状态。现在按照以下规则对门进行处理： 第一次，将所有的门打开； 第二次，将所有编号为 $2$ 的倍数的门作相反的处理（原来是打开的就关闭，原来是关闭的就打开）； 第三次，将所有编号为 $3$ 的倍数的门作相反的处理（原来是打开的就关闭，原来是关闭的就打开）； 以此类推； 第 $N$ 次，将所有编号为 $N$ 的倍数的门作相反的处理（原来是打开的就关闭，原来是关闭的就打开）。 问第 $N$ 次处理后，有多少扇门为打开状态？ 例如：$N=2$，每间教室有 $2$ 扇门，一共有 $4$ 扇门，门编号分别为 $1$、$2$、$3$、$4$ 初始状态：四扇门都为关闭状态； 第一次，将四扇门全部打开； 第二次，将编号为 $2$ 的倍数的门作相反的处理，即将 $2$ 号门和 $4$ 号门关闭。 经过两次处理之后，共有 $2$ 扇门为打开状态。 如下图： [](https://imgtu.com/i/LXF11S) ## 输入格式 输入一个正整数 $N(2 \le N \le 100)$，代表有 $N$ 间教室。 ## 输出格式 按照规则对门进行 $N$ 次处理之后，计算有多少扇门为打开状态并输出。 ```input1 2 ``` ```output1 2 ``` ```input2 10 ``` ```output2 12 ```